Rappelons que l’équation fonctionnelle \( (\mathcal E) \) porte sur des systèmes d’itérations, et a été définie ici. L’exemple que nous proposons repose sur la construction d’un pavage auto-similaire hyperbolique.
Considérons le triangle équilatéral \(T\) du plan hyperbolique d’angles \( (\pi/7, \pi/7, \pi/7) \) représenté sur la figure de une, et formons le patron formé par quatre de ses copies recollées selon la combinatoire indiquée sur la figure qui suit.

Recollons deux nouvelles copies de ce patron dans les deux « coeurs » intérieurs au patron original. On obtient 12 copies du triangle \( T \) recollées suivant la combinatoire dessinée ici :
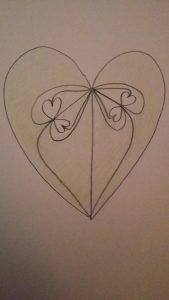
On recommence en collant le patron original dans les quatre « coeurs » intérieurs à cette dernière figure, puis on itère ce procédé une infinité de fois. On obtient un pavage \( \mathcal P \) d’une surface hyperbolique à bord \( S \) homéomorphe à un disque fermé privé d’un ensemble de Cantor.
Il se pourrait a priori que cette surface hyperbolique ait des singularités coniques situés sur le 0-squelette du pavage \( \mathcal P \), mais il n’en est rien. En effet, on vérifie aisément qu’autour de chaque sommet, on a recollé exactement 14 triangles, ce qui fait bien un angle total de \( 14 \times (\pi /7) = 2\pi \).
Le pavage \( \mathcal P \) contient une infinité de copies du triangle \( T\), recollés suivant un procédé auto-similaire. En particulier, on a deux copies \(S_1\) et \(S_2\) de \(S\), qui correspondent aux remplissages des deux coeurs intérieurs du patron original. Ces deux copies sont les images de deux immersions \( h_k : S \rightarrow S_k \) pour \(k= 1,2\).
La surface \(S\) étant planaire, nous pouvons la plonger holomorphiquement dans la sphère de Riemann \( \mathbb P^1(\mathbb C) \). Nous renvoyons au magnifique livre d’Ahlfors-Sario, chapitre 3, paragraphe 4, et nous remercions Peter Haissinsky de nous l’avoir indiqué.
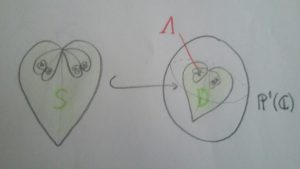
L’image du bord \(\partial S\) par ce plongement sépare la sphère en deux disques topologiques, l’un contenant l’image du plongement ; on le notera \( D\) dans ce qui suit. L’ensemble \( \Lambda := D \setminus S \) est un compact (en fait un ensemble de Cantor) contenu dans la sphère de Riemann. La surface \(\mathbb P^1(\mathbb C)\setminus \Lambda\) appartient à la classe \( O_{AD}\), voir le chapitre 4, partie 1 du livre d’Ahlfors-Sario pour la définition de cette classe. Ceci peut par exemple se déduire du théorème 17E (chapitre 4, partie 5, paragraphe 17) qui s’applique à notre situation sans difficultés. Dans le chapitre 4, partie 1, 4A et 4B, il est montré que \(\Lambda\) est un ensemble effaçable ; une conséquence immédiate est le fait que \( h_1 \) et \(h_2\) se prolongent en des immersions holomorphes de \( D\) dans lui-même.
Le système d’itération obtenu sur le disque \( D \) ne satisfait pas la propriété
\[ h_1 (D) \cap h_2(D) =\emptyset, \]
mais on peut effectuer une petite modification pour se ramener à ce cas. Pour cela, considérons la surface \( D’ \) obtenue à partir de \( D\) en biseautant la « pointe » de \( D \), comme sur la figure suivante.
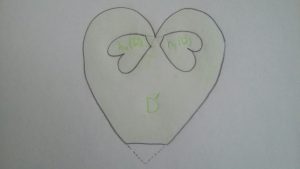
Il s’agit d’une surface de Riemann qui est, comme \( D \), homéomorphe à un disque fermé. Les deux immersions \( h_1 \) et \( h_2 \) envoient \( D’ \) à l’intérieur de lui-même, et les images de \( D’ \) par les \( h_k\) sont disjointes.
En notant \( h_k’\) la restriction de \( h_k\) au disque \( D’\), nous prétendons que le système d’itération \( \{D’, h_1′, h_2′ \}\) vérifie la propriété \( (\mathcal E)\). La démonstration de ce fait se trouve ici.
