Le feuilletage de Hirsch

Nous décrivons dans cette partie un feuilletage qui a été designé par Morris Hirsch. ¹⁾M. Hirsch, A stable analytic foliation with only exceptional minimal sets. in Dynamical Systems, Warwick, 1974, Lect. Notes in Math., 468, Springer-Verlag, 1975, 9C10.

On considère un endomorphisme du cercle \( f :\mathbb S^1 \rightarrow \mathbb S^1\), qui est lisse et admet en tout point une dérivée strictement positive. On traite ici le cas où \(f\) est de degré deux.

Considérons alors un plongement \[  g : D\times \mathbb S^1\rightarrow D\times \mathbb S^1\] du tore solide dans lui-même qui induise \(f\) sur la seconde coordonnée, c’est à dire que \( p\circ g = f\circ p\), où \(p\) est la projection \( D\times \mathbb S^1 \rightarrow \mathbb S^1\). Ici, \( D\) désigne un disque fermé de dimension deux.

 

 

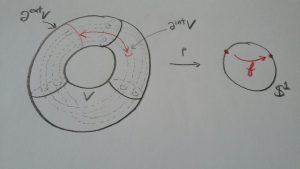
La variété \( V:=   D\times \mathbb S^1 \setminus g (\text{Int} (D\times \mathbb S^1)) \) admet deux composantes de bord. Une extérieure : \(\partial ^{ext} V = \partial D \times \mathbb S^1\),  et l’autre intérieure : \(\partial ^{int} V =g( \partial D \times \mathbb S^1) \). La variété \(W\) obtenue à partir de \(V\) en identifiant la composante extérieure avec la composante intérieure via \(g\) est fermée.

La fibration horizontale sur le tore solide \( \partial D \times \mathbb S^1\) induit une fibration par pantalons sur la variété \( V\), qui se restreint sur chaque composante de bord de \(V \) en une fibration en cercles. Le difféomorphisme \(g\), envoie la fibration en cercles de \(\partial ^{ext} V \) sur celle de \(\partial ^{int} V \). Ainsi, la variété \(W\) admet la structure supplémentaire d’un feuilletage par surfaces : le quotient de la fibration en pantalons sur \(V\). On l’appellera le feuilletage de Hirsch et on le notera \(\mathcal H\).

Ses feuilles sont naturellement décomposées en une union de pantalons, qui sont recollés suivant la combinatoire des grandes orbites de \(f\). Si pour un point \(x\) du cercle \(\mathbb S^1\), on note \( \Pi_x \) la fibre de \(x\) par la restriction de la projection \(p\) à \(V\), les feuilles de  \(\mathcal H\) sont obtenues en recollant les pantalons \(\Pi_x\) où \(x\) décrit une grande orbite de \(f\), comme sur la figure suivante.

 

 

Dans le cas où \(f\) est l’endomorphisme \( t\mapsto 2t\), toutes les feuilles de \(\mathcal H\)  sont denses dans \(W\), car toutes les grandes orbites de \(f\) sont denses dans le cercle. Par contre, il peut arriver que pour d’autres choix de \(f\), le feuilletage \(\mathcal H\) ait un minimal exceptionnel. ²⁾ Un minimal exceptionnel d’un feuilletage de codimension un réel est un ensemble fermé invariant par le feuilletage, dans lequel toutes les feuilles sont denses, et qui est transversalement un ensemble de Cantor. C’est par exemple ce qui se passe si l’on prend \(f\) comme ceci

 

 

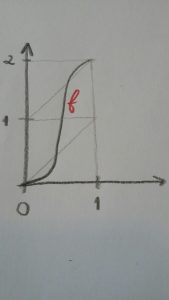
Hirsch prétend que dans ce cas son feuilletage est \(C^1\)-stable, mais il semble y avoir un trou dans son argument : pourquoi après perturbation, la restriction du feuilletage à \(\partial ^{ext} V \sim  \partial ^{int} V \) devrait être une fibration en cercles comme il le prétend, et non un feuilletage quelconque du tore proche de la fibration ?

 

Revenons au cas où \(f=2t\). Dans ce cas, \(f\) admet un unique point fixe \(t=0\). La feuille correspondant à l’orbite de \(0\) est l’union de tous les pantalons dyadiques, comme l’illustre la figure suivante

 

 

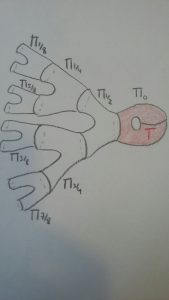
Considérons le tore troué \( T\) qui est l’image de \(\Pi_0\) dans \(W\). En coupant la variété \(W\)  le long de ce tore troué, on obtient une variété à bord et à coin, qui admet pour bord une surface qui est l’union de deux copies du tore troué \(T\) recollées le long de \(\partial T\). On peut s’amuser à les recoller via un difféomorphisme de \(T\) qui préserve l’orientation et qui vaut l’identité sur \(\partial T\). On obtient une nouvelle variété fermée équipée d’un feuilletage qui est un « cousin » du feuilletage de Hirsch. Le lecteur pourra retrouver cette construction ici.