Une famille de feuilletages dyadiques de type Hirsch

IL FAUT REFAIRE LES IMAGES

Donnons nous un système d’itération \( \{D, h_1, h_2\}\), où \(D\) est un disque fermé et où \( h_k:D \rightarrow D\) dont des immersions d’images disjointes. Nous ne supposons pas ici que ces immersions sont holomorphes.

Considérons alors les tores

\[ T_k := \frac{D\setminus h_k (\text{Int}D)}{\partial D\sim h_k(\partial D)},\]

où l’identification \(\sim\) se fait par \( h_k \), et donnons nous un difféomorphisme \(\Phi : T_1 \rightarrow T_2 \) qui en restriction à \( h_2(D) \subset T_1\) est l’application

\[ \Phi _{h_2(D)\subset T_1} = h_1\circ h_2^{-1}: h_2(D)\subset T_1\rightarrow h_1(D)\subset T_2 . \]

Dans ce bloc nous expliquons la construction d’une variété close \(W\) de dimension trois, munie de deux feuilletages transverses \(\mathcal G\) et \(\mathcal H\) de dimension respectives un et deux, avec \(\mathcal H\)  transversalement dyadique. Cette structure induit donc une structure dyadique sur chaque feuille de \(\mathcal G\). Le feuilletage dyadique \(\mathcal H\) s’obtient par chirurgie « longitudinale »¹⁾Voici ce que l’on entend par chirurgie longitudinale le long d’un feuilletage. Prenons une variété équipée d’un feuilletage de codimension un transversalement orienté, et considérons un domaine à bord lisse contenu dans une feuille du feuilletage, qui localement sépare la variété en deux. Considérons un difféomorphisme de ce domaine qui fixe le bord. On coupe la variété le long de ce domaine, et on recolle la partie supérieure à la partie inférieure via le difféomorphisme, pour obtenir une nouvelle variété feuilletée. Attention, après une chirurgie de ce type, on peut éventuellement perdre certaines structures du feuilletage original. Par exemple, si le feuilletage original est lisse, alors le feuilletage obtenu après cette opération sera seulement lisse par morceaux. le long du feuilletage de Hirsch.

 

Partons du produit du pantalon \( D\setminus ( h_1(\text{Int} D) \cup h_2 (\text{Int} D) ) \) par l’intervalle \( [0, 1]  \), représenté sur la figure

Le feuilletage vertical sera a posteriori notre feuilletage \(\mathcal G\), et le feuilletage horizontal par pantalons sera notre feuilletage \(\mathcal H\), la structure transversalement dyadique étant la structure dyadique standard sur l’intervalle \([0,1]\).

Prenons le quotient de ce produit par les identifications

\(     ( z, t ) \sim ( h_2(z) , 2t) \text{  si  } (z,t) \in \partial D \times [0,1/2], \)

et

\(     ( z, t ) \sim ( h_1 (z) , 2t-1) \text{  si  } (z,t) \in \partial D \times [1/2, 1]. \)

On obtient alors une variété de dimension trois compacte à bord et à coin, que l’on note \(V\). Pour voir cela, on observe qu’il y a seulement deux types de points qui posent problème. Les premiers sont les points de \( \partial D \times \{0, 1\} \). Dans le quotient \(V\) ces points sont des points appartenant à la partie lisse du bord de \(V\), comme on peut le constater en visualiser l’illustration suivante

Les points du deuxième type sont les points de \( \partial D \times \{1/2\} \) et sont les plus compliqués. Dans le quotient, ces points appartiennent à un coin, comme le montre la figure

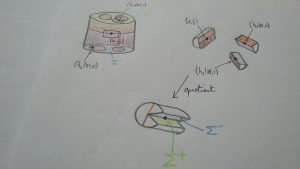
Il s’agit en fait d’un coin d’ « angle » \(2\pi\), où la surface supérieure (en vert sur la figure)

\[ \Sigma ^+ := \frac{D\setminus ( h_1(\text{Int} D) \cup h_2 (\text{Int} D) ) \times \{1\}}{ \partial D \times \{1\} \sim h_1(\partial D) \times  \{1\} }\]

(où \(\sim\) désigne ici l’application \( (h_1 ,2t-1) \) )

rencontre la surface inférieure (en bleue sur la figure)

\[ \Sigma ^- := \frac{D\setminus ( h_1(\text{Int} D) \cup h_2 (\text{Int} D) ) \times \{0\}}{ \partial D \times \{0\} \sim h_2(\partial D) \times  \{0\} }\]

(idem \(\sim\) désigne ici l’application \( (h_2 ,2t) \) )

le long de la courbe fermée simple \( \partial D \times \{1/2\} \).

Or la surface à bord \( \Sigma ^+\)  (resp. \( \Sigma ^-\)) est naturellement identifiée à \( T_1 \setminus h_2(\text{Int}D) \) (resp.  à \( T_2 \setminus h_1(\text{Int}D) \)). Via ces identifications les bords communs des surfaces \(\Sigma^{\pm}\) se recollent via l’application \( h_1\circ h_2^{-1} \) appliquant \( h_2 (\partial D )\sim  \partial \Sigma^+\) sur \(h_1(\partial D )\sim \partial \Sigma^-\).

On peut alors recoller entre elles les surfaces \(\Sigma^{\pm}\)  via le difféomorphisme \(\Phi : \Sigma^+\rightarrow \Sigma^-\) pour obtenir une variété de dimension trois fermée \(W\). Ce faisant, on obtient sur \(W\)  deux  feuilletages \(\mathcal G\) et \(\mathcal H\), qui sont respectivement les quotients du feuilletage vertical et du feuilletage horizontal dans le produit du pantalon par l’intervalle original. Le feuilletage \(\mathcal G\) admet une structure transverse dyadique qu’il hérite de la structure dyadique standard sur l’intervalle \([0,1]\). La construction est achevée.

 

Le feuilletage \(\mathcal H\) est un « cousin » du feuilletage de Hirsch associé à l’endomorphisme \( f= 2t\). En effet, considérons un système d’itération sur le disque unité qui soit tel que \( h_2 = i\circ h_1\), où \( i : D\rightarrow D \) est une involution préservant l’orientation avec un unique point fixe en dehors des images des \(h_k\).  Considérons également un difféomorphisme \( \Phi : D\rightarrow D\) qui soit égal à l’identité près de \(\partial D\) et à \(i\) sur un voisinage de l’union des \(h_k(D)\) (un demi-twist de Dehn le long de \(\partial D\) par exemple). Ce difféomorphisme induit naturellement un difféomorphisme de \( T_1 \) dans \(T_2 \)  qui est égal à \(h_1\circ h_2^{-1}\) en restriction à \(h_2(D)\subset T_1\). La variété feuilletée \(W\) obtenue en recollant \(\Sigma^-\) à \(\Sigma^+\) via ce difféomorphisme est le feuilletage de Hirsch construit ici.   En particulier, toutes les feuilles de \(\mathcal H\) sont denses dans \(W\).