Nous montrons ici que le système d’itération présenté là vérifie bien la propriété \( (\mathcal E)\).
Le tore \( T_k\) est obtenu en quotientant \( D’ \setminus h_k'(\text{Int}(D’)) \) via la relation \( z’\sim h_k'(z’)\) si \( z’\in \partial D’\). En fait, on s’assure aisément que \(T_k\) est également le quotient de \( D \setminus h_k(\text{Int}(D)) \) par la relation \(z\sim h_k(z)\) si \( z\in \partial D\). (voir à ce propos la relation sur les systèmes d’itération, présentée ici)
Le tore \( T_1 \) est donc formé d’une partie constituée de quatre triangles isométriques au triangle hyperbolique d’angles \(( \pi/7,\pi/7,\pi/7) \), et d’une copie de \( h_2(D) \), collés suivant la combinatoire représentée sur la figure suivante
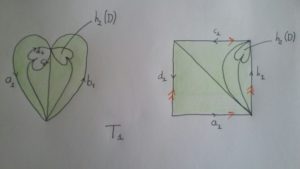
De même, le tore \( T_2 \) est formé d’une partie constituée de quatre triangles \(( \pi/7,\pi/7,\pi/7) \), et d’une copie de \( h_1(D) \), collés suivant la combinatoire représentée sur la figure suivante

On constate que dans le revêtement universel \( \tilde{T_2}\) de \(T_2\), le domaine fondamental suivant a exactement la même combinatoire que celle apparaissant dans la construction de \( T_1 \) :

Ainsi, l’équation fonctionnelle \( (\mathcal E) \) est bien satisfaite dans ce cas, ce que nous voulions établir.
Notons \(\Phi\) le biholomorphisme entre \(T_1\) et \( T_2\) qui étend \( h_1\circ h_2^{-1} \) en restriction à \( h_2(D) \subset T_1 \). Il est intéressant de comprendre la classe d’homotopie de \(\Phi\), et notamment quelle est la configuration des classes d’homologie \( \Phi_* \gamma_1 \) et \(\gamma_2 \) dans \(H_1(T_2,\mathbb Z)\), où \( \gamma_k \) est par définition la classe de la courbe \(\partial D\sim h_k (\partial D) \) dans \( T_k\), munie de l’orientation directe induite par \(\partial D\). Ces classes sont représentées sur la figure suivante

qui complète les figures précédentes. Dans la base \( [a_2], [b_2] \) de \(H_1(T_2,\mathbb Z)\), on obtient donc
\[ \Phi_* \gamma_1 = (1,2) \text{ et } \gamma_2 = (1,-1) . \]
Dans la base \( [a_2+2 b_2] , [b_2] \), on a
\[ \Phi_* \gamma_1 = (1,0) \text{ et } \gamma_2 = (1,-3) . \]