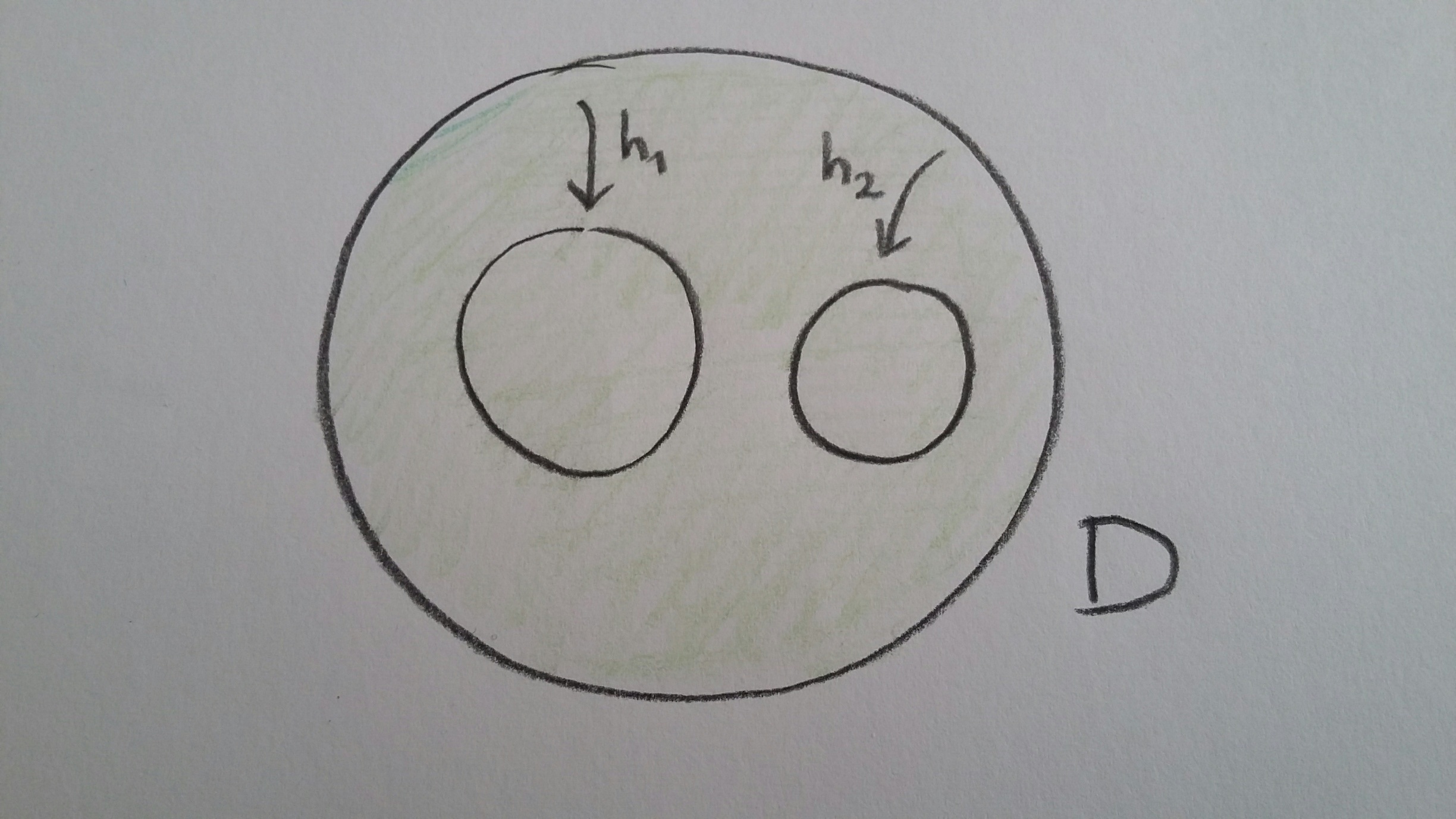
Soit \( D\) une surface de Riemann compacte à bord difféomorphe à un disque fermé. On se donne un système d’itération formé par deux applications holomorphes injectives \[ h_k: D \rightarrow \text{Int} (D),\ \ \ k= 1,2\] telles que l’intersection \(h_1(D)\cap h_2(D) \) est vide.
Chaque application \( h_k \) contracte la métrique de Poincaré par un facteur \(<1\) par le lemme de Schwarz, et admet donc un unique point fixe \( z_k \) dans l’intérieur de \(D \). Le cas d’un système d’itération plus général sera traité dans un autre bloc.
Pour chaque \( k= 1,2\), on note \( T_k \) le quotient de \( D\setminus \{z_k\} \) par la relation \( z \sim h_k(z)\). Il s’agit de l’ « espace des orbites » de \( h_k \) en restriction à \(D\setminus \{z_k\} \) ; ce sont des courbes elliptiques, obtenues à partir de l’anneau \( D \setminus \text{Int} (h_k (D) ) \) en recollant ses deux composantes de bord \( \partial D \) et \( h_k (\partial D)\) par \( h_k\).
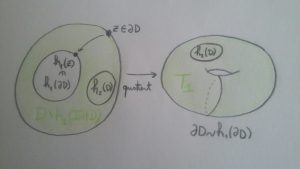
On observe alors que \( h_2(D) \) peut être vu comme une sous-partie de \( T_1 \), et vice versa (c’est à dire que \(h_1(D) \) peut être vu comme une sous-partie de \(T_2 \) ). On s’intéresse ici à l’équation fonctionnelle suivante :
\( (\mathcal E) \) La transformation
\[ h_1\circ h_2^{-1} : h_2(D) \subset T_1 \rightarrow h_1(D) \subset T_2 \]
se prolonge en un biholomorphisme de \( T_1 \) dans \( T_2\).
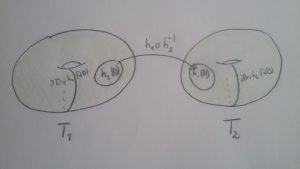
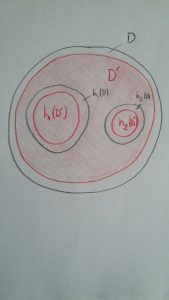
L’équation fonctionnelle \( (\mathcal E) \) est « invariante » par la relation suivante sur les systèmes d’itération. Par exemple considérons le système d’itération \( \{D’, h_1′, h_2′ \} \), où \(D’ \) est un domaine simplement connexe contenu dans \(D\) et contenant \(h_1(D)\) et \(h_2(D)\), et où \( h_k’ \) désigne la restriction de \( h_k \) à \(D’ \). Alors on voit immédiatement que le système \( \{D’, h_1′, h_2′ \} \) vérifie l’équation \( (\mathcal E) \) ssi le système original \( \{D, h_1, h_2 \} \) la vérifie également.
Evidemment, une classe de systèmes d’itération ne satisfait pas en général une équation fonctionnelle telle que \( (\mathcal E) \), comme nous le verrons bientôt. D’ailleurs, nous ne connaissons pour l’instant qu’un seul exemple de tel système, que nous avons découvert par expérimentations numériques sur l’équation de Jouanolou, et que nous présentons ici.